A polygon is defined by a collection of rings. Each ring is a collection of contiguous line segments such that the start point and the end point are the same.
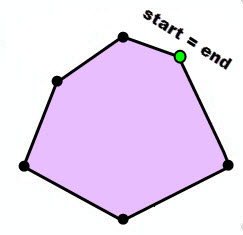
Boundary and Rings
The boundary of a polygon is the collection of rings by which the polygon is defined. The boundary contains one or more outer rings and zero or more inner rings. An outer ring is oriented clockwise while an inner ring is oriented counterclockwise. Imagine walking clockwise along an outer ring. The area to your immediate right is the interior of the polygon and to your left is the exterior.
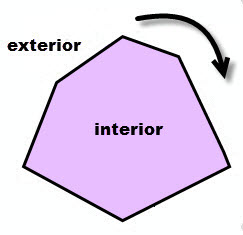
Similarly, if you were to walk counter-clockwise along an inner ring, the area to your immediate right is the interior of the polygon and to your left is the exterior.
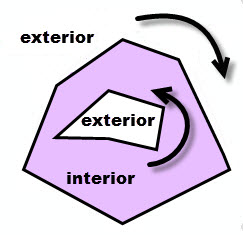
It is important to understand the boundary, interior and exterior of a geometry when using the various operators. The relational operators, for example, rely heavily on these concepts.
If a polygon has an inner ring, the inner ring looks like a hole. If the hole contains another outer ring, that outer ring looks like an island.
 |
 |
 |
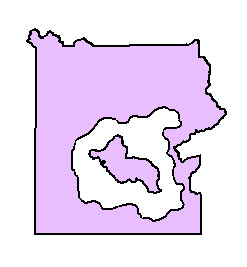 |
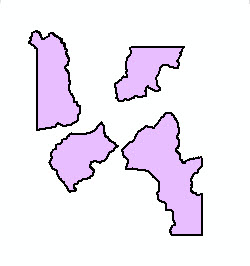
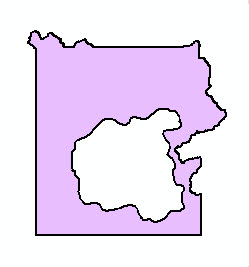
| 1 outer ring, no inner rings | 4 outer rings, no inner rings | 1 outer ring, 1 inner ring | 2 outer rings, 1 inner ring |
Valid polygons
A valid polygon has the main property such that for every polygon segment the polygon exterior is unambiguously to the left of the segment, and the polygon interior is unambiguously to the right of the segment.
As a result of the above property the following is also true:
- segments can touch other segments only at the end points,
- segments have non-zero length,
- outer rings are clockwise and holes are counterclockwise,
- each polygon ring has non-zero area.
- order of the rings does not matter,
- rings can be self-tangent,
- rings can not overlap.
A valid polygon is said to be simple. See the What is a simple polygon? for a more detailed specification of simple polygons. Note that a simple polygon may not be OGC simple. See the Simplify operator with OGC restrictions.
Examples
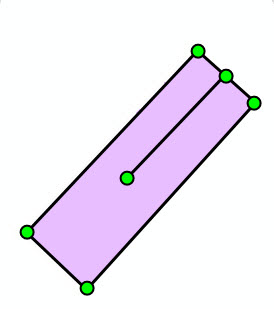
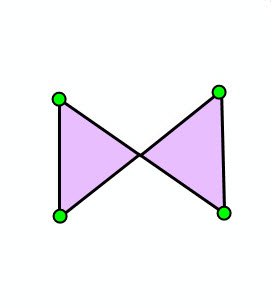
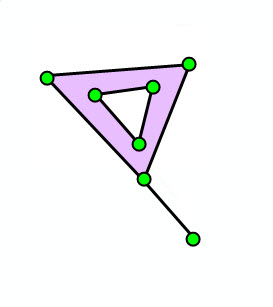
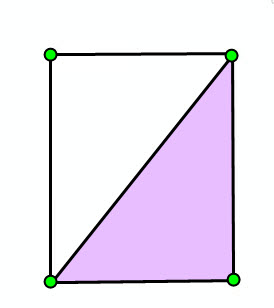
Let's look at some examples of non-simple vs. simple polygons. The green circles are the vertices of the polygon, and the lavender colored area represents the interior of the polygon.
| Non-simple polygons | ||||
|---|---|---|---|---|
 |
 |
 |
 |
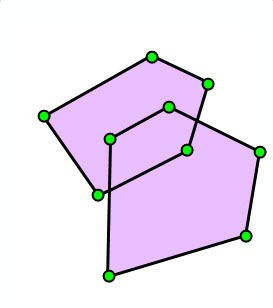 |
| Self-intersection | Self-intersection | Dangling segment | Dangling segment | Overlapping rings |
| Simple polygons | ||||
|---|---|---|---|---|
 |
 |
 |
 |
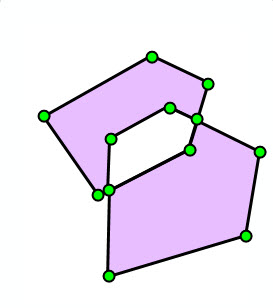 |
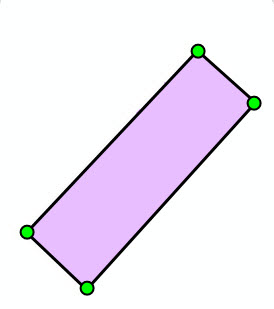
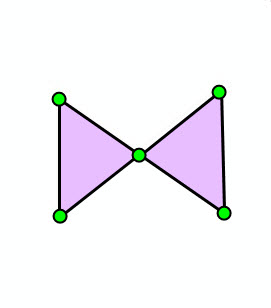
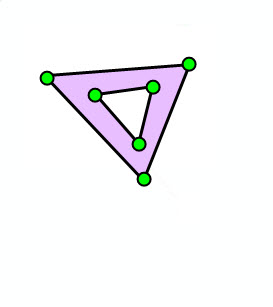
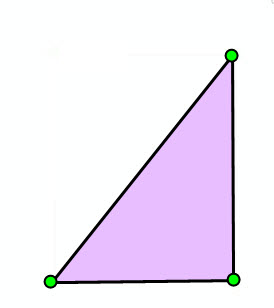
| No self-intersection | Self-intersection at vertex | No dangling segment | No dangling segment | No overlapping rings |
When drawing a polygon, use the even-odd fill rule. The even-odd fill rule will guarantee that the polygon will draw correctly even if the ring orientation is not as described above for simple polygons.
JSON format
A polygon can be represented as a JSON string. A polygon in JSON format contains an array of rings
and an optional spatialReference. A polygon can also have boolean-valued hasM and hasZ fields. The default value is false
for both the hasM and hasZ fields.
Each ring is represented by an array of points. Exterior rings are oriented clockwise, while interior rings are oriented counter-clockwise. The order of the rings is irrelevant. The first point of each ring is always the same as the last point. Each point in a ring is represented as an array of numbers. See the description of JSON multipoints for details on the interpretation of the point arrays.
An empty polygon is represented with an empty array for the rings field.
Syntax
{
"hasZ" : true | false,
"hasM" : true | false,
"rings": [
[[<x11>,<y11>,<z11>,<m11>],[<x12>,<y12>,<z12>,<m12>], ... ,[<x1j>,<y1j>,<z1j>,<m1j>]],
... ,
[[<xn1>,<yn1>,<zn1>,<mn1>],[<xn2>,<yn2>,<zn2>,<mn2>], ... ,[<xnk>,<ynk>,<znk>,<mnk>]]
],
"spatialReference" : {"wkid" : <wkid>}
}
2D Polygon
{
"rings": [
[[6453,16815],[10653,16423],[14549,5204],[-7003,6939],[6453,16815]],
[[914,7992],[3140,11429],[1510,10525],[914,7992]]
],
"spatialReference" : {"wkid" : 54004}
}
3D Polygon with Ms
Note that the third point does not have a z-value, and the second ring does not have any m-values.
{
"hasZ" : true,
"hasM" : true,
"rings": [
[[6453,16815,35,1],[10653,16423,36,2],[14549,5204,null,3],[-7003,6939,37,4],[6453,16815,35,1]],
[[914,7992,30],[3140,11429,29],[1510,10525,28],[914,7992,30]]
],
"spatialReference" : {"wkid" : 54004}
}
Empty Polygon
{"rings": []}
Creating a polygon
To create a polygon, we can use the Polygon class methods or one of the import operators.
Each of the code samples below creates a polygon with two outer rings and one inner ring.
The polygon looks like this:
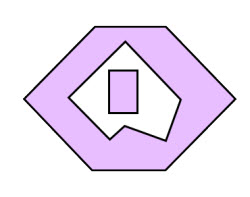 |
| Create this polygon |
Polygon class methods
When using the Polygon class methods to create a polygon, the order in which the rings are created
doesn't matter. What matters is the ring orientation. Remember, clockwise implies an outer ring whereas
counter-clockwise implies an inner ring.
To begin each ring, we call the startPath method and then successive calls to the
lineTo method. We don't need to repeat the start point as the end point.
public static Polygon createPolygon1()
{
Polygon poly = new Polygon();
// clockwise => outer ring
poly.startPath(0, 0);
poly.lineTo(-0.5, 0.5);
poly.lineTo(0, 1);
poly.lineTo(0.5, 1);
poly.lineTo(1, 0.5);
poly.lineTo(0.5, 0);
// hole
poly.startPath(0.5, 0.2);
poly.lineTo(0.6, 0.5);
poly.lineTo(0.2, 0.9);
poly.lineTo(-0.2, 0.5);
poly.lineTo(0.1, 0.2);
poly.lineTo(0.2, 0.3);
// island
poly.startPath(0.1, 0.7);
poly.lineTo(0.3, 0.7);
poly.lineTo(0.3, 0.4);
poly.lineTo(0.1, 0.4);
return poly;
}
Import from JSON
As with the Polygon class methods, when using OperatorImportFromJson
to create a polygon the order in which the rings are created doesn't matter. What matters is the
ring orientation. Unlike the Polygon class methods, the start point of each ring must
be repeated to specify the end point.
The code shown below creates the same polygon as before, but notice that the inner ring that forms the hole is given before the outer ring. This was done just to drive home the point that the order of the rings doesn't matter when the polygon is in JSON format.
static Polygon createPolygonFromJson() throws JsonParseException, IOException
{
String jsonString = "{\"rings\":[[[0.5,0.2],[0.6,0.5],[0.2,0.9],[-0.2,0.5],[0.1,0.2],[0.2,0.3],[0.5,0.2]],"
+ "[[0.0,0.0],[-0.5,0.5],[0.0,1.0],[0.5,1.0],[1.0,0.5],[0.5,0.0],[0.0,0.0]],"
+ "[[0.1,0.7],[0.3,0.7],[0.3,0.4],[0.1,0.4],[0.1,0.7]]],"
+ " \"spatialReference\":{\"wkid\":4326}}";
MapGeometry mapGeom = OperatorImportFromJson.local().execute(Geometry.Type.Polygon, jsonString);
return (Polygon)mapGeom.getGeometry();
}
Import from GeoJSON
Unlike the Polygon class methods and OperatorImportFromJson, when using
OperatorImportFromGeoJson to create a polygon the order in which the rings are given
does matter. Within an array of rings, the outer ring is always first followed by zero or more
inner rings. However, the order of the arrays of rings doesn't matter. The start point of each
ring must be repeated to specify the end point.
The code shown below creates the same polygon as in the previous examples.
static Polygon createPolygonFromGeoJson() throws JsonParseException, IOException
{
String geoJsonString = "{\"type\":\"MultiPolygon\","
+ "\"coordinates\":[[[[0.0,0.0],[-0.5,0.5],[0.0,1.0],[0.5,1.0],[1.0,0.5],[0.5,0.0],[0.0,0.0]],"
+ "[[0.5,0.2],[0.6,0.5],[0.2,0.9],[-0.2,0.5],[0.1,0.2],[0.2,0.3],[0.5,0.2]]],"
+ "[[[0.1,0.7],[0.3,0.7],[0.3,0.4],[0.1,0.4],[0.1,0.7]]]],"
+ "\"crs\":\"EPSG:4326\"}";
MapGeometry mapGeom = OperatorImportFromGeoJson.local().execute(GeoJsonImportFlags.geoJsonImportDefaults, Geometry.Type.Polygon, geoJsonString, null);
return (Polygon)mapGeom.getGeometry();
}
Import from WKT
As with OperatorImportFromGeoJson, when using OperatorImportFromWkt
to create a polygon the order in which the rings are given does matter. Within an array of rings,
the outer ring is always first followed by zero or more inner rings. However, the order of the arrays
of rings doesn't matter. The start point of each ring must be repeated to specify the end point.
The code shown below creates the same polygon as in the previous examples, but notice that the outer ring that forms the island is given first. This was done for illustrative purposes. It could have been given last, which probably would be more understandable to the reader.
static Polygon createPolygonFromWKT() throws JsonParseException, IOException
{
String wktString = "MULTIPOLYGON (((0.1 0.7, 0.1 0.4, 0.3 0.4, 0.3 0.7, 0.1 0.7)),"
+ "((0 0, 0.5 0, 1 0.5, 0.5 1, 0 1, -0.5 0.5, 0 0),"
+ "(0.5 0.2, 0.2 0.3, 0.1 0.2, -0.2 0.5, 0.2 0.9, 0.6 0.5, 0.5 0.2)))";
Geometry geom = OperatorImportFromWkt.local().execute(WktImportFlags.wktImportDefaults, Geometry.Type.Polygon, wktString, null);
return (Polygon)geom;
}
Extracting Outer Rings
Many workflows require getting only the outer rings of a polygon.
The method getAllOuterRings extracts all the outer rings of a polygon. The call to
OperatorSimplifyOGC makes sure there are no self-intersections, all outer rings are
clockwise, and holes are counterclockwise. You can skip the call to OperatorSimplifyOGC
if you trust your input polygon.
static List<Polygon> getAllOuterRings(Polygon polygon)
{
Polygon simplePolygon = (Polygon)OperatorSimplifyOGC.local().execute(polygon, null, true, null);
ArrayList<Polygon> rings = new ArrayList<Polygon>();
int n = simplePolygon.getPathCount();
for (int i = 0; i < n; i++)
{
if (simplePolygon.calculateRingArea2D(i) <= 0)
continue;
Polygon ring = new Polygon();
ring.addPath(simplePolygon, i, true);
rings.add(ring);
}
return rings;
}
The method getOutermostRings extracts the outermost rings, that is,
only rings that are not contained inside of any hole.
static List<Polygon> getOutermostRings(Polygon polygon)
{
List<Polygon> allOuterRings = getAllOuterRings(polygon);
GeometryCursor outerRingsCursor = new SimpleGeometryCursor(allOuterRings);
GeometryCursor unionCursor = OperatorUnion.local().execute(outerRingsCursor, null, null);
Geometry unionPoly = unionCursor.next();
// Holes could have been produced during the union, so rerun just in case.
return getAllOuterRings((Polygon)unionPoly);
}